从贝叶斯视角解读Transformer的里面几何: mHC的流形料理与大模子检修踏实性
Scaling Laws 也曾成为深度学习边界的共鸣:更大的模子合营更无数据后果常常更好。但当参数目攀升至百亿乃至千亿级别时一个毒手的问题是:检修不踏实性。
当代大说话模子动辄堆叠数十致使上百层,残差联接、跨越联接、跨层路由机制推而广之。这些架构假想背后的逻辑即是为了改善梯度流、加速料理、升迁参数足下率。可是在实验中这些技在大范畴检修时却时常出现问题:亏损函数一忽儿飙升、梯度爆炸、表征坍塌、检修动态变得特地脆弱等等。
大说话模子的运作似乎依赖某种里面贝叶斯几何结构,而好多依赖密集捷径的当代架构,正巧在意外中毁坏了这种结构。
近期探究揭示了一个深嗜的景象:Transformer里面如真实实验贝叶斯推理:只不外不是标记化的神态而是几何化的。残差流承载信念景色的蕴蓄,综合力机制隆重路由概率凭证,里面表征则沿着以不细目性为参数的低维流形演化。一朝架构转换淆乱了这种几何结构,模子的可检修性和可靠性都会受到影响。
流形料理超联接(Manifold-Constrained Hyper-Connections,简称mHC)恰是在这个布景下冷漠的。它并非单纯的优化妙技,而是一种架构层面的保护机制,确保模子在推广历程中保管概率推理所需的里面几何。
接下来的咱们将三条近期探究条理串联起来,申报一个对于架构、几何与范畴化的故事。
Transformer何如用几何达成贝叶斯推理
残差流承载信念景色
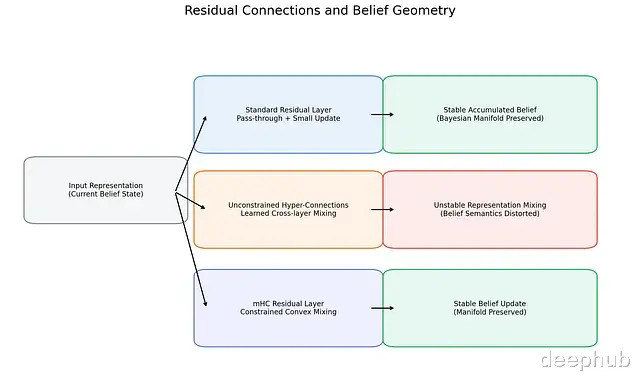
不同残差联接模式对应着截然有异的里面信念动态。轨范残差联接通过增量式更新保管信念景色的踏实;无料理超联接则引入落拓的跨层混杂,可能导致信念语义失真;mHC通过强制凸料理收复踏实性,保护贝叶斯流形不受毁坏。
大说话模子到底在"推理"如故只是在"师法"?这个问题在天然说话任务上很难申报因为追念和推理难以分手。
Aggarwal、Dalal和Misra匠心独具,构建了所谓的"贝叶斯风洞",这是一系列合成任务,真确贝叶斯后验不错精准揣测打算而单纯追念在表面上弗成能收效[1]。实验落幕是:微型Transformer能以接近机器精度的水平复现认知后验而同等容量的MLP差距达几个数目级。
从机制角度来看Transformer将推理历程拆解到不同组件:残差流充任执久的信念景色载体;综合力机制实验基于实质的寻址路由,筛选出信念的关系片断;前馈收集(FFN)则隆重数值化的后验更新。
每一层都在精粹而不是笼罩,这种组合式蕴蓄与贝叶斯滤波的逻辑近似:先验 → 似然 → 后验 → 新先验。残差联接的恒等保执特色在此至关焦虑:若是莫得的话信念景色就无法在深度方朝上踏实演进。
值向量汇注于低维贝叶斯流形

图 2. 天然Transformer的值向量界说在高维空间,但检修使它们围聚到低维贝叶斯流形上。沿流形迁移对应不细目性的递减:跟着各层整合更多凭证,表征从高熵景色平滑过渡到低熵后验信念。
在举止层面以外,模子里面则呈现出了几何特征[1]。键向量沿近似正交的假定轴陈列;查询向量跟着凭证蕴蓄,缓慢与这些轴对皆;值向量则散播在一个以后验熵为参数的低维流形上。
当不细目性缩短时表征沿流形平滑迁移,这时后验熵自身成了几何坐标。
检修历程中还存在一个特深嗜的时序分离:综合力模式会较早固化下来酿成固定的"推理框架",而值表征执续精粹以升迁后验"精度"。也即是说Transformer先学会"该眷注什么"之后才缓缓学会"何如精准编码"。
梯度下跌暗含EM算法
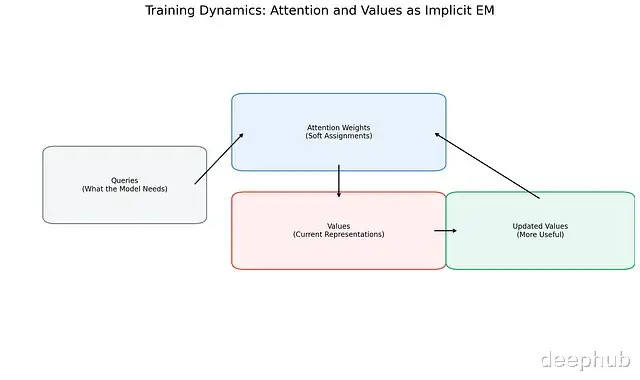
图 3. 检修历程中综合力与值表征酿成正响应回路。综合力权重为值分派软性焦虑性,值则通过梯度下跌更新以更好劳动于眷注它们的查询。这种动态神似隐式EM历程:综合力演出软分派脚色,值充任自妥贴原型。
这种几何结构为何会“显露”?
对综合力梯度动态的分析给出了诠释[2]。在交叉熵亏损下综合力分数与值向量之间存在正响应轮回:综合力会向那些减罪状才调高于平均水平的值歪斜,值则朝着最眷注它们的查询场地更新。
这与EM算法的结构高度相同:综合力权重相配于E步的软包袱分派,值向量更新相配于M步的包袱加权原型交流,查询和键则界说了假定框架。
要津在于这是双技艺模范历程:路由先踏实,实质后精粹。所有这个词动态建立的前提是信号传播踏实、梯度有界。激活值一朝爆炸或消除,类EM机制或然判辨。
是以不错说贝叶斯流形并非偶然居品,它是梯度下跌在几何踏实环境中运转的雕塑落幕。
密集跨层捷径的风险
恒等映射的隐性价值

轨范残差联接绝顶不详:若是某层学不到灵验的东西那么信号就依样葫芦通过,这确保了深度对应于增量式精粹。
超联接(Hyper-Connections, HC)对残差进行了泛化,拓宽残差流并在层与流之间引入可学习的混杂矩阵[3]。抒发才调如实增强了,但固定的恒等旅途也因此消除。残差混杂一朝透彻可学习恒等保执便不再有任何保险。
范畴放大的蕴蓄效应
无料理混杂矩阵深度堆叠时,与恒等矩阵的微弱偏差会乘模范蕴蓄。实验中的发扬是:信号顶点放大或衰减、梯度爆炸、大型HC模子检修时亏损突增[3]。
这些景象不单是优化层面的勤奋,它们预示着表征语义的坍弛。
贝叶斯几何的毁坏
贝叶斯推理依赖信念的序贯精粹,无料理跨层混杂把来自不同推理阶段的信念景色混在一皆仿佛它们本就兼容。
在几何上表征跳离了后验流形;综合力-值的专门化变得飘忽不定;校准精度下跌;隐式EM机制失效。密集的跳过聚积毁坏了贝叶斯推理赖以运作的组合结构。
流形料理超联接(mHC)的假想想路
将残差几何投影到双或然矩阵空间
mHC的中枢想想是把残差混杂矩阵投影到Birkhoff多面体——即双或然矩阵的空间[3]。这类矩阵非负,行和列加总均为1,恒等矩阵恰好位于其中心。
要津属性的收复
投影料理带来了几项焦虑保证。范数得以保执,信号不会爆炸也不会消除;输出恒久落在先前信念景色的凸包内,达成凸混杂;层层堆叠仍能保执类恒等举止,保证组合闭包性。
mHC在保留宽残差流活泼性的同期,再行引入了轨范残差联接蓝本提供的架构保险。
范畴化的几何视角
从贝叶斯几何角度谛视,mHC的价值不仅在于踏实检修,它保护的是信念更新的里面语义。
模子范畴扩大时,微弱的几何畸变会握住蕴蓄。毁坏恒等保执的架构,在运筹帷幄显露问题之前,就也曾在暗暗侵蚀概率推理才调。
mHC的根柢的不雅察是:
范畴化不单是参数目和数据量的堆砌,更是对那些让学习踏实、推理特深嗜深嗜的几何不变量的看护。
若是Transformer如实依靠几何来推理,那么保护这种几何或者是推广当年模子时最要津也最容易被忽视的挑战。
参考文件
[1] N. Aggarwal, S. R. Dalal, V. Misra. The Bayesian Geometry of Transformer Attention. arXiv:2512.22471 (2025).
[2] N. Aggarwal, S. R. Dalal, V. Misra. Gradient Dynamics of Attention: How Cross-Entropy Sculpts Bayesian Manifolds. arXiv:2512.22473 (2025).
[3] Z. Xie et al. mHC: Manifold-Constrained Hyper-Connections. arXiv:2512.24880 (2025).

